In order to model human migration we use a partial differential equation (PDE) approach on networks. When it comes to modelling human migration since the last glacial maximum until the mid holocene, the two most widely used approaches are agent-based and PDE-based approaches. The agent-based approach focuses on micro-scale phenomena, while a PDE-approach can model macroscopic migration events [K]. Since we are interested in large scale migration events, we chose the PDE approach.
For the specific case of human migration, a PDE model is chosen where the underlying domain is a network. For a PDE model, the underlying domain, i.e., the space where we want to model human migration, could be an entire landmass like Europe. However, small scale movements of humans in Europe are not relevant in the context of large scale migration events which would happen along migration routes. Consequently, human migration is modelled on a network consisting of vertices connected by migration routes. For the vertices of the network, we chose places of known human presence based on archaeological data.
As an example of how to imagine the network approach, think of a trade network, where you want to model the exchange and distribution of raw materials between settlement sites. Once you have zoomed out enough (imagine the trade network of an entire country), it no longer matters whether the trader walked on the right or the left side of a path. Accordingly, we treat human migration on a large scale.
In order to formulate the migration process in a mathematical model, we use a diffusion-advection-type PDE. It consists of four terms, each describing different parts of the migration process. The first part models how a human population changes over time. Next we add an advection term which describes human migration due to some kind of incentive, like, for example, resource availability along coastlines. Seemingly random movements are described by a diffusion term.
In order to include the population growth, we add a last term which is referred to as logistic growth term. All these terms interact with each other to describe the population dynamics over time on our network:
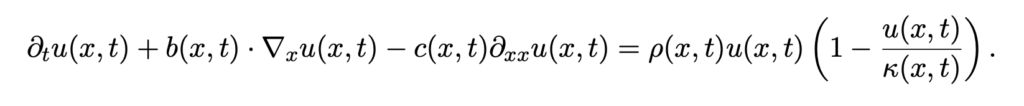
There are plenty of challenges in successfully implementing this model. This starts with the network itself. Since there is no migration network template available, this has to be created in an initial step. We can use archaeological data from existing databases [CRC] and mathematical tools for network creation [DG]. The current progress of the creation of a migration network is shown in [PB].
Additionally, the parameters of the advection-diffusion model need to be filled with as much information on human presence as possible in order to obtain most accurate results. Eventually this will result in a large model that can describe human dynamics between the last glacial maximum and the mid holocence.
References
[CRC] I. Schmidt, (2021): CRC806_E1_AUR_Sites_Database_20210331. CRC806-Database, University of Cologne, DOI: 10.5880/SFB806.63
[DG] C. Dettmann, O. Georgio (2016): Random geometric graphs with general connection functions, Phys. Rev. E, Vol. 92, No. 3, pp. 032313.
[K] K. Klein, (2022): Simulating Palaeolithic Human Dispersal Using Human Existence Potential and Constrained Random Walk Model. Dissertation, University of Cologne, Institute for Geophysics and Meteorology, http://kups.ub.uni-koeln.de/id/eprint/62239.
[PB] L. Perlberg, M. Brockmann, Creating migration networks based on archaeological data using least-cost-path analysis, Poster, Rhein-Ruhr-Workshop, January 2025, DOI:10.5880/SFB806.63.2
Source image blog teaser: Unsplash

